LESSON 010
加速度センサーを繊細に使いこなす
前回micro:bit の加速度センサーについて説明しましたが、アプリケーションに用意された傾きを知らせるブロックや関数を用いると傾きをジェスチャーされて傾きをジェスチャーされますが、傾きが60度以上ないと判定されないため、2方向の傾きを同時に判定することはできません。そこでx、y、zのそれぞれの加速度の値を測定し活用する方法を検討しましょう
micro:bitでは、
を測定出来ます。
micro:bitでは、
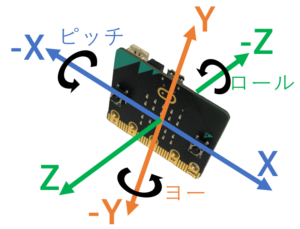
を測定出来ます。
x、y方向の加速度の値を用いて8方向の傾きで下がっている方にLEDの点灯し教える水平器を作ります。
MakeCode
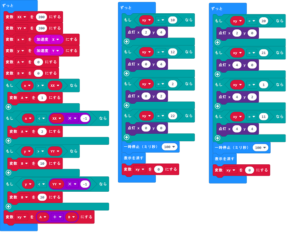
Python Editor スケッチ《 Mtest024》
from microbit import *
while True:
A=0
B=0
xx=200
yy=200
x=accelerometer.get_x()
y=accelerometer.get_y()
if x > xx:
A=1
if xx < -1*x:
A=2
if y > yy:
B=10
if yy < -1*y:
B=20
xy=A+B
if xy==20:
display.set_pixel(2,0,9)
if xy==21:
display.set_pixel(4,0,9)
if xy==1:
display.set_pixel(4,2,9)
if xy==11:
display.set_pixel(4,4,9)
if xy==10:
display.set_pixel(2,4,9)
if xy==12:
display.set_pixel(0,4,9)
if xy==2:
display.set_pixel(0,2,9)
if xy==22:
display.set_pixel(0,0,9)
sleep(100)
display.clear()解説
accelerometer.get_x()
加速度センサーのx方向の加速度の値
accelerometer.get_y()
加速度センサーのy方向の加速度の値
accelerometer.get_z()
加速度センサーのz方向の加速度の値
xx・yy
x・y のしきい値
感度を変えるならココの部分
MakeCode
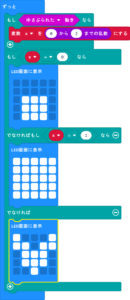
Python Editor スケッチ《 Mtest025》
import random
while True:
if accelerometer.was_gesture('shake'):
x=random.randint(0, 2)
if x == 0 :
display.show(Image('00000:'
'00000:'
'09990:'
'09990:'
'09990'))
if x == 1 :
display.show(Image('99999:'
'99999:'
'99999:'
'99999:'
'99999'))
if x == 2 :
display.show(Image('90009:'
'99099:'
'09990:'
'09990:'
'00900'))解説
import random
random.randint(最小値, 最大値)
最小値, 最大値の間で乱数を発生させる。
加速度センサーが感知し回数を知らせる
ジャンケンマシーンので使用した”ゆさぶられた”では感度が悪いため加速度の”絶対値”を使うことで高感度で個々に合った万歩計が作れます。
今回は5歩でスマイルが出るようにしました。
Aボタンで回数を表示
Bボタンで回数のリセット
ジャンケンマシーンので使用した”ゆさぶられた”では感度が悪いため加速度の”絶対値”を使うことで高感度で個々に合った万歩計が作れます。
今回は5歩でスマイルが出るようにしました。
Aボタンで回数を表示
Bボタンで回数のリセット
MakeCode
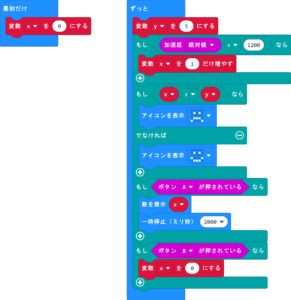
Python Editor スケッチ《 Mtest026》
from microbit import *
import math
a=0
while True:
x = accelerometer.get_x()
y = accelerometer.get_y()
z = accelerometer.get_z()
xyz = int(math.sqrt(x**2 + y**2 + z**2))
if xyz > 2000:
a +=1
sleep(100)
if a < 5:
display.show(Image.SAD)
else:
display.show(Image.HAPPY)
if button_a.was_pressed():
display.scroll(a)
sleep(500)
if button_b.was_pressed():
a=0解説
math.sqrt(x**2 + y**2 + z**2)
\( xyz={\sqrt{x^{2}+y^{2}+z^{2}}} \)
3D(X 軸 Y 軸 Z軸)加速度の合成加速度ベクトルが xyz になります。
=INT(数値)
INT関数は引数の小数点以下を切り捨て
リンク








